算法框架思维
数据结构的存储方式
算法底层其实都是数组和链表
队列,栈这些都可以使用链表也可以使用数组实现
图的邻接表也就是链表,邻接矩阵也就是二维数组
树用数组实现就是堆,因为堆是一个完全二叉树
用链表实现就是很常见的那种「树」,因为不一定是完全二叉树,所以不适合用数组存储
数组:在中间插入删除元素需要迁移,耗费时间。可以通过索引快速访问呢对应的元素。紧凑连续存储节约空间,但是如果要扩容就要重新分配空间再把所有数据复制进行o(N)
链表:插入删除只是改改指针,但是没办法随机访问,索引访问元素效率也很低。而且每个元素需要存储前后的指针更加占空间
数据结构基本操作
任何数据结构做的也就是增删查改。也就是遍历+访问
数组遍历
1
2
3
4
5
| void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
}
}
|
链表遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class ListNode {
int val;
ListNode next;
}
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
}
}
void traverse(ListNode head) {
traverse(head.next);
}
|
二叉树遍历
1
2
3
4
5
6
7
8
9
10
|
class TreeNode {
int val;
TreeNode left, right;
}
void traverse(TreeNode root) {
traverse(root.left);
traverse(root.right);
}
|
N叉树遍历
1
2
3
4
5
6
7
8
9
10
|
class TreeNode {
int val;
TreeNode[] children;
}
void traverse(TreeNode root) {
for (TreeNode child : root.children)
traverse(child);
}
|
这个N叉树遍历也可以扩展图的遍历,图就是好几条N叉树,图有可能出现环,加上一个visited做标记
算法的本质
我觉得基本算法的本质就是穷举
二叉树系列算法
二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案
这两种问题也对应着回溯算法和动态规划算法
遍历二叉树得出答案
我们需要计算二叉树的最大深度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
int res = 0;
int depth = 0;
int maxDepth(TreeNode root) {
traverse(root);
return res;
}
void traverse(TreeNode root) {
if (root == null) {
res = Math.max(res, depth);
return;
}
depth++;
traverse(root.left);
traverse(root.right);
depth--;
}
}
|
用 traverse 函数遍历了一遍二叉树的所有节点,维护 depth 变量,在叶子节点的时候更新最大深度。
分解问题得出答案
计算二叉树深度这个问题,我们可以分解成计算左子树的最大深度和右子树的最大深度,计算左子树和右子树最大深度的max值
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
int res = Math.max(leftMax, rightMax) + 1;
return res;
}
|
二叉树的前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| List<Integer> res = new LinkedList<>();
List<Integer> preorder(TreeNode root) {
traverse(root);
return res;
}
void traverse(TreeNode root) {
if (root == null) {
return;
}
res.add(root.val);
traverse(root.left);
traverse(root.right);
}
|
也就是在二叉树的前序位置上进行遍历
这里我们应用分解问题的方式

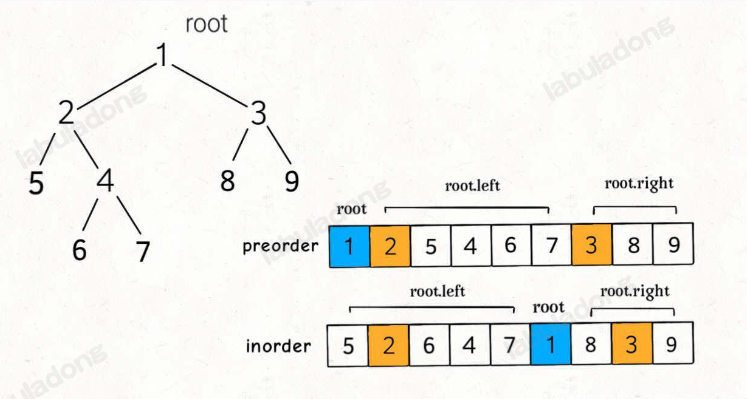
前序遍历的结果,根节点的值在第一位,后面接着左子树的前序遍历结果,最后接着右子树的前序遍历结果。
那么我们就可以把遍历二叉树前序拆成,根节点+遍历左子树+遍历右子树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
List<Integer> preorder(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
res.add(root.val);
res.addAll(preorder(root.left));
res.addAll(preorder(root.right));
return res;
}
|
BFS算法
也就是二叉树的层序遍历
图论的算法也就是二叉树算法的延续