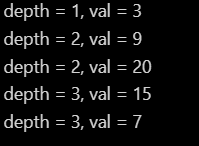算法基础-数据结构基础(二)
二叉树
二叉树绝对是最重要的数据结构,没有之一
1
2
3
4
5
6
7
8
| 1
/ \
2 3
/ / \
4 5 6
/ \
7 8
|
每个节点下方直接相连的节点称为子节点,上方直接相连的节点称为父节点。比方说节点 3 的父节点是 1,左子节点是 5,右子节点是 6;节点 5 的父节点是 3,左子节点是 7,没有右子节点。
我们称最上方那个没有父节点的节点 1 为根节点,称最下层没有子节点的节点 4、7、8 为叶子节点。
我们称从根节点到最下方叶子节点经过的节点个数为二叉树的最大深度/高度,上面这棵树的最大深度是 4,即从根节点 1 到叶子节点 7 或 8 的路径上的节点个数。
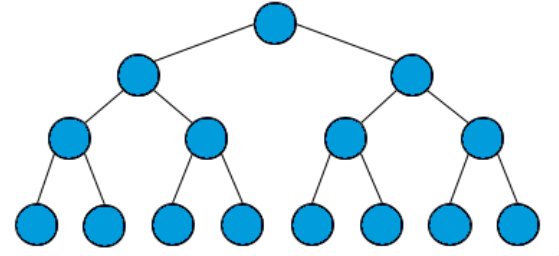
满二叉树

满二叉树的节点计算是
设深度为 h,那么总节点数就是 2^h - 1
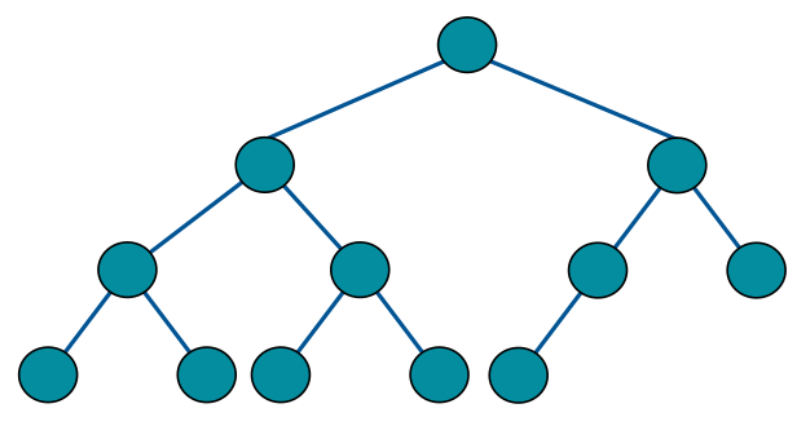
完全二叉树

每一层的节点都紧凑靠左排列,且除了最后一层,其他每层都必须是满的
完全二叉树的特点:由于它的节点紧凑排列,如果从左到右从上到下对它的每个节点编号,那么父子节点的索引存在明显的规律。
二叉搜索树(BST)
左子树的每个节点的值都要小于这个节点的值,右子树的每个节点的值都要大于这个节点的值。你可以简单记为「左小右大」
下面这个树就是一个BST
1
2
3
4
5
| 7
/ \
4 9
/ \ \
1 5 10
|
这里我们需要考虑的是整棵子树的所有节点,不能只看一部分
下面这个树就不是一个BST
该看整棵子树,注意看节点 7 的左子树中有个节点 8,比 7 大,这就不符合 BST 的定义了。
1
2
3
4
5
6
| 7
/ \
4 9
/ \ \
1 8 10
|
BST 是非常常用的数据结构。因为左小右大的特性,可以让我们在 BST 中快速找到某个节点,或者找到某个范围内的所有节点
比方说,对于一棵普通的二叉树,其中的节点大小没有任何规律可言,那么你要找到某个值为 x 的节点,只能从根节点开始遍历整棵树。
而对于 BST,你可以先对比根节点和 x 的大小关系,如果 x 比根节点大,那么根节点的整棵左子树就可以直接排除了,直接从右子树开始找,这样就可以快速定位到值为 x 的那个节点。
二叉树的实现方式
类似于链表的链式结构进行存储
1
2
3
4
5
6
| public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { this.val = x; }
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);
|
二叉树的递归/层序遍历
递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| let preorderResult = [];
let inorderResult = [];
let postorderResult = [];
function traverse(root) {
if (root === null) {
return;
}
preorderResult.push(root.val);
traverse(root.left);
inorderResult.push(root.val);
traverse(root.right);
postorderResult.push(root.val);
}
let allRoot = TreeNode.create([1, 2, 3, null, 4, 5, 6]);
traverse(allRoot);
|
这里的代码是javascript代码,create创建一个二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| 1
/ \
2 3
\ / \
4 5 6
preorderResult = 124356 也就是12null4(1)356
inorderResult = 241536
中序遍历的顺序是从中间然后中间的左子节点,右子节点,主节点,然后右侧的中间节点的左子节点,然后中间节点,然后右子节点
也就是应该是2 null 4 1 5 3 6 (1)
postorderResult = 425631 也就是null 4 2 5 6 3 1
|
这种格式的二叉树
然后调用traverse方法进行遍历
层序遍历
用队列的方式实现二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
System.out.println(cur.val);
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
let result = levelOrderTraverse(TreeNode.create([3,9,20,null,null,15,7]));
|
还有一种常见的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
System.out.println("depth = " + depth + ", val = " + cur.val);
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}
|
控制台输出:

其实第二种的使用更加的广泛,因为节点的层数信息很重要
多叉树的递归/层序遍历
二叉树是每个节点都有两个子节点
多叉树是每个节点都有任意的子节点
下面是二叉树的节点
1
2
3
4
5
| class TreeNode {
int val;
TreeNode left;
TreeNode right;
}
|
下面是多叉树的节点
1
2
3
4
| class Node {
int val;
List<Node> children;
}
|
递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
traverse(root.right);
}
void traverse(Node root) {
if (root == null) {
return;
}
for (Node child : root.children) {
traverse(child);
}
}
|
多叉树没有中序位置,所以没有中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| let preorderResult = [];
let postorderResult = [];
function traverse(root) {
if (root === null) {
return;
}
preorderResult.push(root.val);
for (let child of root.children) {
traverse(child);
}
postorderResult.push(root.val);
}
let allRoot = Node.create([1,null,3,2,4,null,5,6]);
traverse(allRoot);
|
1
2
3
| preorderResult = 135624
postorderResult = 563241
|
层序遍历
多叉树的层序遍历和二叉树的层序遍历一样,都是用队列来实现
第一种写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void levelOrderTraverse(Node root) {
if (root == null) {
return;
}
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
Node cur = q.poll();
System.out.println(cur.val);
for (Node child : cur.children) {
q.offer(child);
}
}
}
|
第二种写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void levelOrderTraverse(Node root) {
if (root == null) {
return;
}
Queue<Node> q = new LinkedList<>();
q.offer(root);
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
System.out.println("depth = " + depth + ", val = " + cur.val);
for (Node child : cur.children) {
q.offer(child);
}
}
depth++;
}
}
|
图结构基础及通用代码实现
图结构就是多叉树的延申
多叉树只能是父节点指向子节点,图结构是可以互相指的
图的逻辑结构
图是由节点和边组成的

图的逻辑结构用代码实现:
1
2
3
4
5
|
class Vertex {
int id;
Vertex[] neighbors;
}
|
这种结构和多叉树其实差不多
但是这种结构是逻辑上的,具体实现使用邻接表,邻接矩阵实现
度的概念
图里面有一个度的概念
度就是每个节点相连的边的条数。
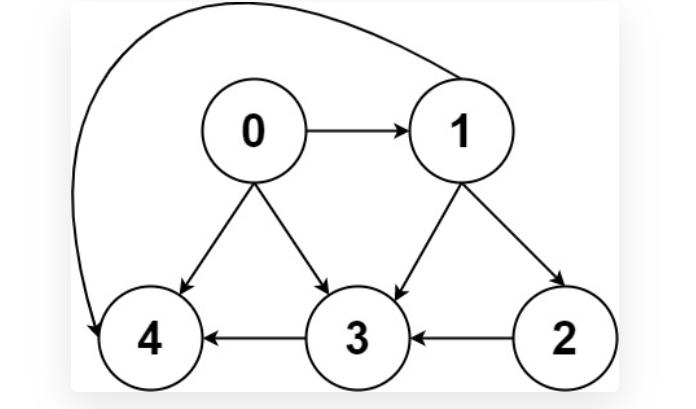
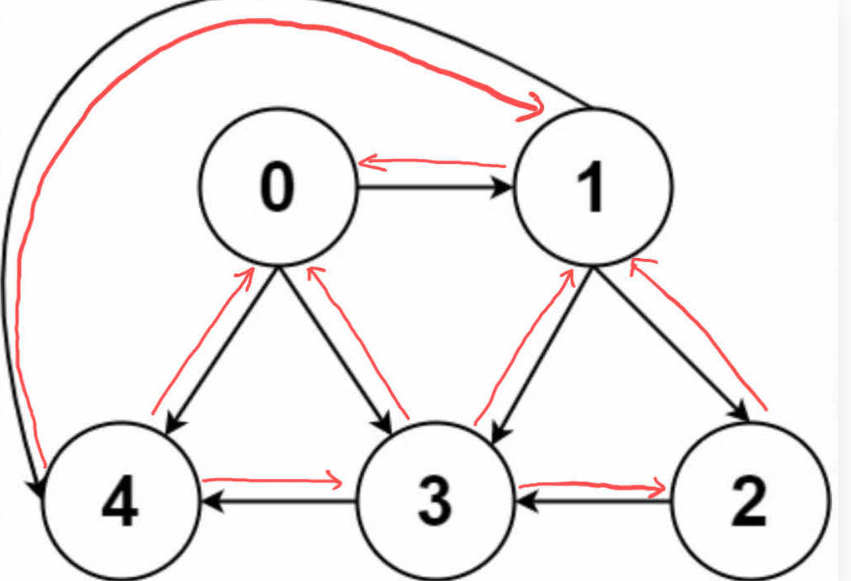
入度就是有几条边指向这个节点,出度就是它有几条边指向其他节点。比如节点3的入度就是3,出度就是1
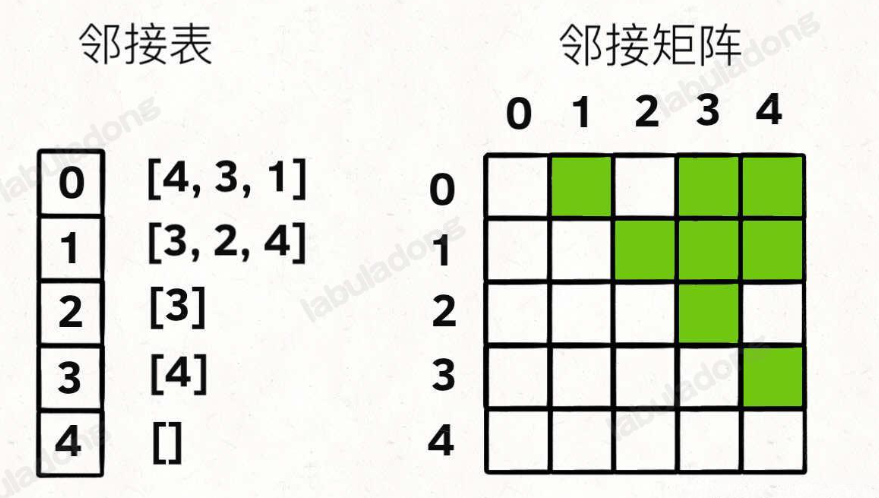
邻接表和邻接矩阵

邻接表底层是一个数组,一个数组里面来存放的节点的权重和连接信息
节点类型不一定都是int的,也可能是其他类型,如果图节点是其他类型,比如字符串等,就可以额外使用一个哈希表,把实际节点和整数id映射起来
邻接表和邻接矩阵的使用场景
后面的算法中,邻接表的使用多一些
邻接矩阵的最大优势就是矩阵可以进行数学计算
有向和加权
加权的实现就是在邻接表中我们不仅仅存储某个节点x的邻居节点,还存储x到每个邻居的权重
有向就是有方向的,从哪到哪,无向就是双向的
下面就是无向图

有向加权图的邻接表实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
class WeightedDigraph {
public static class Edge {
int to;
int weight;
public Edge(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
private List<Edge>[] graph;
public WeightedDigraph(int n) {
graph = new List[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
}
public void addEdge(int from, int to, int weight) {
graph[from].add(new Edge(to, weight));
}
public void removeEdge(int from, int to) {
for (int i = 0; i < graph[from].size(); i++) {
if (graph[from].get(i).to == to) {
graph[from].remove(i);
break;
}
}
}
public boolean hasEdge(int from, int to) {
for (Edge e : graph[from]) {
if (e.to == to) {
return true;
}
}
return false;
}
public List<Edge> neighbors(int v) {
return graph[v];
}
public static void main(String[] args) {
WeightedDigraph graph = new WeightedDigraph(3);
graph.addEdge(0, 1, 1);
graph.addEdge(1, 2, 2);
graph.addEdge(2, 0, 3);
graph.addEdge(2, 1, 4);
System.out.println(graph.hasEdge(0, 1));
System.out.println(graph.hasEdge(1, 0));
graph.neighbors(2).forEach(edge -> {
System.out.println(2 + " -> " + edge.to + ", wight: " + edge.weight);
});
graph.removeEdge(0, 1);
System.out.println(graph.hasEdge(0, 1));
}
}
|
有向加权图(邻接矩阵实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| import java.util.ArrayList;
import java.util.List;
public class WeightedDigraph {
public static class Edge {
int to;
int weight;
public Edge(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
private int[][] matrix;
public WeightedDigraph(int n) {
matrix = new int[n][n];
}
public void addEdge(int from, int to, int weight) {
matrix[from][to] = weight;
}
public void removeEdge(int from, int to) {
matrix[from][to] = 0;
}
public boolean hasEdge(int from, int to) {
return matrix[from][to] != 0;
}
public List<Edge> neighbors(int v) {
List<Edge> res = new ArrayList<>();
for (int i = 0; i < matrix[v].length; i++) {
if (matrix[v][i] > 0) {
res.add(new Edge(i, matrix[v][i]));
}
}
return res;
}
public static void main(String[] args) {
WeightedDigraph graph = new WeightedDigraph(3);
graph.addEdge(0, 1, 1);
graph.addEdge(1, 2, 2);
graph.addEdge(2, 0, 3);
graph.addEdge(2, 1, 4);
System.out.println(graph.hasEdge(0, 1));
System.out.println(graph.hasEdge(1, 0));
graph.neighbors(2).forEach(edge -> {
System.out.println(2 + " -> " + edge.to + ", wight: " + edge.weight);
});
graph.removeEdge(0, 1);
System.out.println(graph.hasEdge(0, 1));
}
}
|
有向无权图(邻接表/邻接矩阵实现)
直接复用上面的 WeightedDigraph 类就行,把 addEdge 方法的权重参数默认设置为 1 就行了
无向加权图(邻接表/邻接矩阵实现)
直接复用上面用邻接表/领接矩阵实现的 WeightedDigraph 类就行了,只是在增加边的时候,要同时添加两条边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class WeightedUndigraph {
private WeightedDigraph graph;
public WeightedUndigraph(int n) {
graph = new WeightedDigraph(n);
}
public void addEdge(int from, int to, int weight) {
graph.addEdge(from, to, weight);
graph.addEdge(to, from, weight);
}
public void removeEdge(int from, int to) {
graph.removeEdge(from, to);
graph.removeEdge(to, from);
}
public boolean hasEdge(int from, int to) {
return graph.hasEdge(from, to);
}
public List<WeightedDigraph.Edge> neighbors(int v) {
return graph.neighbors(v);
}
public static void main(String[] args) {
WeightedUndigraph graph = new WeightedUndigraph(3);
graph.addEdge(0, 1, 1);
graph.addEdge(1, 2, 2);
graph.addEdge(2, 0, 3);
graph.addEdge(2, 1, 4);
System.out.println(graph.hasEdge(0, 1));
System.out.println(graph.hasEdge(1, 0));
graph.neighbors(2).forEach(edge -> {
System.out.println(2 + " <-> " + edge.to + ", wight: " + edge.weight);
});
graph.removeEdge(0, 1);
System.out.println(graph.hasEdge(0, 1));
System.out.println(graph.hasEdge(1, 0));
}
}
|
无向无权图(邻接表/邻接矩阵实现)
直接复用上面的 WeightedUndigraph 类就行,把 addEdge 方法的权重参数默认设置为 1 就行了
图结构的DFS-BFS遍历
DFS就是递归遍历
BFS就是层序遍历
总结
图的遍历就是
多叉树遍历 的延伸。主要的遍历方式还是深度优先搜索(DFS)和广度优先搜索(BFS)。唯一的区别是,树结构中不存在环,而图结构中可能存在环,所以我们需要标记遍历过的节点,避免遍历函数在环中死循环。
具体来说,遍历图的所有「节点」时,需要 visited 数组在前序位置标记节点;遍历图的所有「路径」时,需要 onPath 数组在前序位置标记节点,在后序位置撤销标记。
如果题目说这幅图不存在环,那么图的遍历就完全等同于多叉树的遍历。
遍历节点
对比多叉树来看一下图节点的遍历过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Node {
int val;
List<Node> children;
}
void traverse(Node root) {
if (root == null) {
return;
}
System.out.println("visit " + root.val);
for (Node child : root.children) {
traverse(child);
}
}
|
假设多叉树的结构如下
1
2
3
4
5
6
| A
/ \
B C
/ \ \
D E F
|
目标节点为 E。假设当前遍历到节点 B,此时路径 path 为 [A, B]。
目标节点为 E。节点的值和结构如下:
A (根节点)
B
D
E (目标节点)
C
F
初始化:
path 初始化为空。
调用 traverse(A, E) 开始遍历。
访问节点 A
root 为 A,path 更新为 [A]。
检查 A.val 是否等于 E.val,不相等。
遍历 A 的子节点 B 和 C。
访问节点B
递归调用 traverse(B, E)。
root 为 B,path 更新为 [A, B]。
检查 B.val 是否等于 E.val,不相等。
遍历 B 的子节点 D 和 E。
访问节点D
递归调用 traverse(D, E)。
root 为 D,path 更新为 [A, B, D]。
检查 D.val 是否等于 E.val,不相等。
D 没有子节点,递归返回到 B。
移除 D,path 恢复为 [A, B]。
1
2
| 当前路径: [A, B, D]
回溯到: [A, B]
|
访问节点E
递归调用 traverse(E, E)。
root 为 E,path 更新为 [A, B, E]。
检查 E.val 是否等于 E.val,相等。
找到目标节点,输出路径 [A, B, E]。
E 没有子节点,递归返回到 B。
移除 E,path 恢复为 [A, B]。
1
2
3
| 当前路径: [A, B, E]
找到目标路径: [A, B, E]
回溯到: [A, B]
|
回到节点 A 并访问 C
B 的子节点遍历完毕,递归返回到 A。
移除 B,path 恢复为 [A]。
递归调用 traverse(C, E)。
root 为 C,path 更新为 [A, C]。
检查 C.val 是否等于 E.val,不相等。
遍历 C 的子节点 F。
1
2
3
| 当前路径: [A, B]
回溯到: [A]
当前路径: [A, C]
|
访问节点F
递归调用 traverse(F, E)。
root 为 F,path 更新为 [A, C, F]。
检查 F.val 是否等于 E.val,不相等。
F 没有子节点,递归返回到 C。
移除 F,path 恢复为 [A, C]。
1
2
| 当前路径: [A, C, F]
回溯到: [A, C]
|
结束遍历
C 的子节点遍历完毕,递归返回到 A。
移除 C,path 恢复为 [A]。
A 的子节点遍历完毕,递归结束。
最终路径 path 为空。
1
2
3
| 当前路径: [A, C]
回溯到: [A]
遍历结束
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Vertex {
int id;
Vertex[] neighbors;
}
boolean[] visited;
void traverse(Vertex s) {
if (s == null) {
return;
}
if (visited[s.id]) {
return;
}
visited[s] = true;
System.out.println("visit " + s.id);
for (Vertex neighbor : s.neighbors) {
traverse(neighbor);
}
}
|
这里的图遍历比多叉树的遍历多了一个visited数组,用来记录被遍历过的节点,避免遇到环的时候进行死循环
遍历路径
而对于图结构来说,由起点 src 到目标节点 dest 的路径可能不止一条。我们需要一个 onPath 数组,在进入节点时(前序位置)标记为正在访问,退出节点时(后序位置)撤销标记,这样才能遍历图中的所有路径,从而找到 src 到 dest 的所有路径:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
boolean[] onPath = new boolean[graph.size()];
List<Integer> path = new LinkedList<>();
void traverse(Graph graph, int src, int dest) {
if (src < 0 || src >= graph.size()) {
return;
}
if (onPath[src]) {
return;
}
onPath[src] = true;
path.add(src);
if (src == dest) {
System.out.println("find path: " + path);
}
for (Edge e : graph.neighbors(src)) {
traverse(graph, e.to, dest);
}
path.remove(path.size() - 1);
onPath[src] = false;
}
|
示例
初始状态:
- onPath = [false, false, false, false]
- path = []
开始遍历:
- 调用 traverse(graph, 0, 3)
- 当前节点 0 被添加到路径,onPath[0] 设置为 true
访问节点 1:
- 调用 traverse(graph, 1, 3)
- 当前节点 1 被添加到路径,onPath[1] 设置为 true
访问节点 3:
- 调用 traverse(graph, 3, 3)
- 当前节点 3 被添加到路径,路径 0 -> 1 -> 3 被找到并打印
- 返回到上一步,节点 3 被移出路径,onPath[3] 设置为 false
返回节点 0,访问节点 2:
- 调用 traverse(graph, 2, 3)
- 当前节点 2 被添加到路径,onPath[2] 设置为 true
访问节点 3:
- 调用 traverse(graph, 3, 3)
- 当前节点 3 被添加到路径,路径 0 -> 2 -> 3 被找到并打印
- 返回到上一步,节点 3 被移出路径,onPath[3] 设置为 false
关键
这里的关键就是之前的遍历节点不许与撤销数组的标记,但是这里需要在后序位置撤销标记
因为前文遍历节点的代码中,visited 数组的指责是保证每个节点只会被访问一次。而对于图结构来说,要想遍历所有路径,可能会多次访问同一个节点,这是关键的区别。
图结构的BFS遍历
图结构的广度优先遍历其实就是多叉树的层序遍历,只不过是需要一个数组来避免遍历节点
一般BFS算法也就是这个广度的层序遍历是来计算最短路径的,如果要求所有的路径一般使用DFS算法
如果只求最短路径的话,只需要遍历「节点」就可以了,因为按照 BFS 算法一层一层向四周扩散的逻辑,第一次遇到目标节点,其实就是最短路径。
下面是两种遍历的两种写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
void levelOrderTraverse(Node root) {
if (root == null) {
return;
}
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
Node cur = q.poll();
System.out.println(cur.val);
for (Node child : cur.children) {
q.offer(child);
}
}
}
void bfs(Graph graph, int s) {
boolean[] visited = new boolean[graph.size()];
Queue<Integer> q = new LinkedList<>();
q.offer(s);
visited[s] = true;
while (!q.isEmpty()) {
int cur = q.poll();
System.out.println("visit " + cur);
for (Edge e : graph.neighbors(cur)) {
if (!visited[e.to]) {
q.offer(e.to);
visited[e.to] = true;
}
}
}
}
|
记录步数的写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
void levelOrderTraverse(Node root) {
if (root == null) {
return;
}
Queue<Node> q = new LinkedList<>();
q.offer(root);
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
System.out.println("depth = " + depth + ", val = " + cur.val);
for (Node child : cur.children) {
q.offer(child);
}
}
depth++;
}
}
void bfs(Graph graph, int s) {
boolean[] visited = new boolean[graph.size()];
Queue<Integer> q = new LinkedList<>();
q.offer(s);
visited[s] = true;
int step = 0;
while (!q.isEmpty()) {
int cur = q.poll();
System.out.println("visit " + cur + " at step " + step);
for (Edge e : graph.neighbors(cur)) {
if (!visited[e.to]) {
q.offer(e.to);
visited[e.to] = true;
}
}
step++;
}
}
|
二叉堆
二叉堆的基本原理
二叉堆的基本操作只有两个,一个下沉(sink)和一个上浮(swim)
二叉树的主要应用有两个,一个是很有用的数据结构优先队列,另一个是排序方法堆排序
什么是二叉堆
二叉堆就是一个能动态排序的数据结构
也就是说我们可以不断的向这个数据结构中添加或者删除数据,数据结构会自动的调节元素的位置,让我们可以有序的读取元素
能动态排序的常用数据结构其实只有两个,一个是优先级队列(底层用二叉堆实现),另一个是二叉搜索树。二叉搜索树的用途更广泛,优先级队列能做的事情,二叉搜索树其实都能做。但优先级队列的 API 和代码实现相较于二叉搜索树更简单,所以一般能用优先级队列解决的问题,我们没必要用二叉搜索树。
二叉堆的分类
二叉堆分为大顶堆和小顶堆
二叉堆是一种特殊的二叉树,这棵二叉树上的任意节点的值,都必须大于等于(或小于等于)其左右子树所有节点的值。如果是大于等于,我们称之为「大顶堆」,如果是小于等于,我们称之为「小顶堆」。
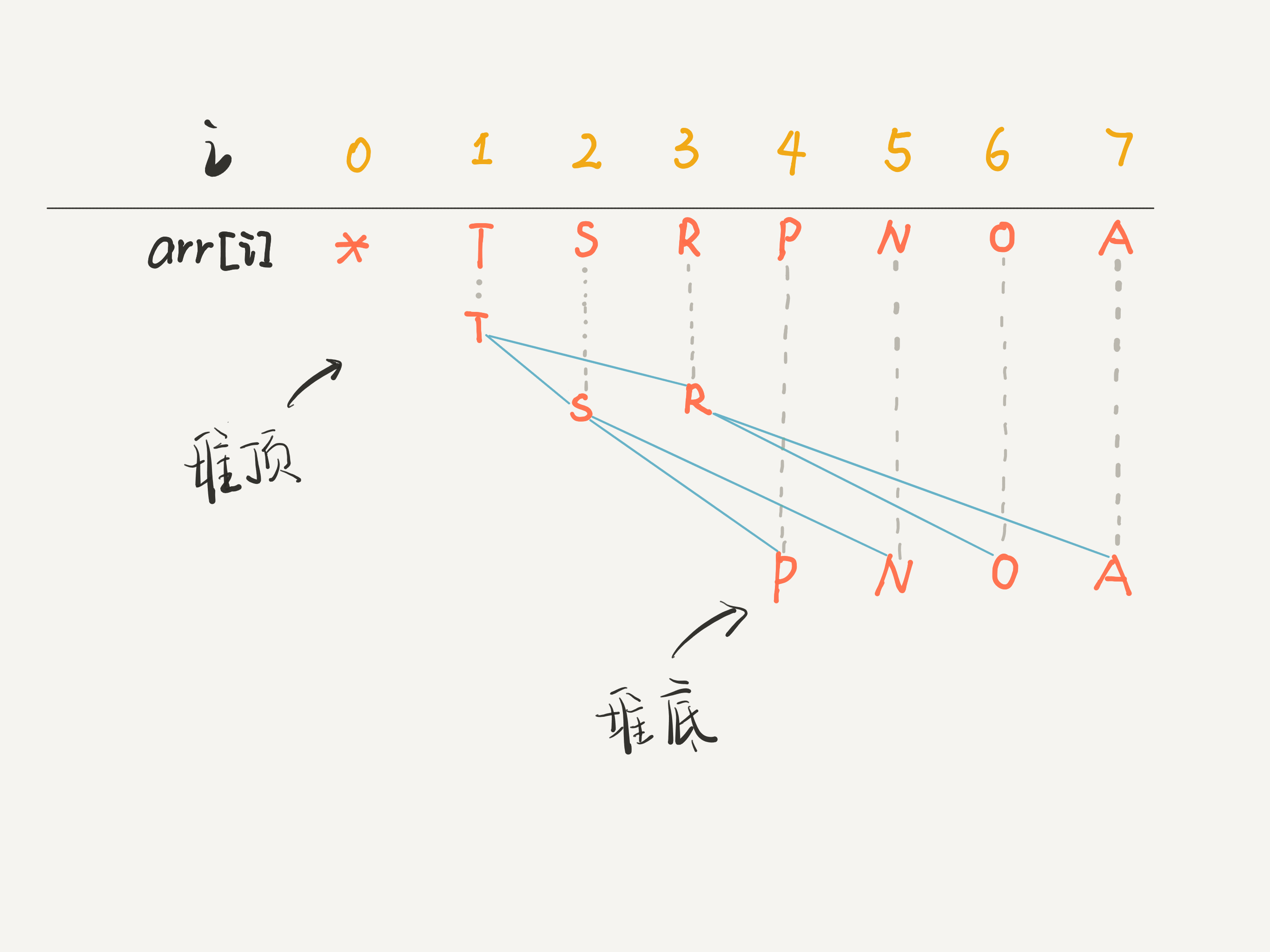
那么小顶堆中,根节点就是整棵树上的最小值,大顶锥中根节点就是整棵树上的最大值
最常见的应用
优先级队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class MyPriorityQueue {
void push(int x);
int peek();
int pop();
int size();
}
|
自动排序的代价就是这个时间复杂度是nlogn。虽然它的api很像队列,但是和队列没有关系,底层和二叉树有关
堆排序
相当于把一个乱序的数组都 push 到一个二叉堆(优先级队列)里面,然后再一个个 pop 出来,就得到了一个有序的数组
1
2
3
4
5
6
7
8
9
10
11
12
|
int[] heapSort(int[] arr) {
int[] res = new int[arr.length];
MyPriorityQueue pq = new MyPriorityQueue();
for (int x : arr)
pq.push(x);
for (int i = 0; i < arr.length; i++)
res[i] = pq.pop();
return res;
}
|
push 方法插入元素
以小顶堆为例,向小顶堆中插入新元素遵循两个步骤:
1、先把新元素追加到二叉树底层的最右侧,保持完全二叉树的结构。此时该元素的父节点可能比它大,不满足小顶堆的性质。
2、为了恢复小顶堆的性质,需要将这个新元素不断上浮(swim),直到它的父节点比它小为止,或者到达根节点。此时整个二叉树就满足小顶堆的性质了。
pop方法删除元素
以小顶堆为例,删除小顶堆的堆顶元素遵循两个步骤:
1、先把堆顶元素删除,把二叉树底层的最右侧元素摘除并移动到堆顶,保持完全二叉树的结构。此时堆顶元素可能比它的子节点大,不满足小顶堆的性质。
2、为了恢复小顶堆的性质,需要将这个新的堆顶元素不断下沉(sink),直到它的子节点比它小为止,或者到达叶子节点。此时整个二叉树就满足小顶堆的性质了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
let minHeap = Heap.createMinHeap([1,6,8,2,10,13,0,7]);
let topNode = minHeap;
let bottomNode = minHeap.left.left.left;
let parent = bottomNode.parent;
bottomNode.parent = null;
if (parent.left === bottomNode) {
parent.left = null;
} else {
parent.right = null;
}
topNode.val = bottomNode.val;
let p = topNode;
while (p.left || p.right) {
let min = p;
if (p.left !== null && p.left.val < min.val) {
min = p.left;
}
if (p.right !== null && p.right.val < min.val) {
min = p.right;
}
if (min === p) break;
let temp = p.val;
p.val = min.val;
min.val = temp;
p = min;
}
console.log('min heap recovered');
|
peek 方法查看堆顶元素
直接查看根节点的值就行
在数组上模拟二叉树
实际上在代码的实现上不会用类似二叉树的方法来实现节点,而是使用数组的方式来模拟二叉树的结构
因为最主要的原因,时间复杂度的原因,之前我们描述的push和pop方法的操作过程中的第一步是需要找到二叉树最底层的最右侧的元素。
正常情况下需要层序遍历或者递归遍历二叉树,时间复杂度是o(N),这种肯定不可以
如果想要用数组来模拟二叉树,前提是这个二叉树必须是完全二叉树
完全二叉树就是除了最后一层,其他层的节点都是满的,最后一层的节点都靠左排列。

1
2
3
4
5
6
7
8
9
10
11
12
|
int parent(int node) {
return node / 2;
}
int left(int node) {
return node * 2;
}
int right(int node) {
return node * 2 + 1;
}
|
我们直接在数组的末尾追加元素,就相当于在完全二叉树的最后一层从左到右依次填充元素;数组中最后一个元素,就是完全二叉树的底层最右侧的元素,完美契合我们实现二叉堆的场
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| class SimpleMinPQ {
private final int[] heap;
private int size;
public SimpleMinPQ(int capacity) {
heap = new int[capacity + 1];
size = 0;
}
public int size() {
return size;
}
int parent(int node) {
return node / 2;
}
int left(int node) {
return node * 2;
}
int right(int node) {
return node * 2 + 1;
}
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
public int peek() {
return heap[1];
}
public void push(int x) {
heap[++size] = x;
swim(size);
}
public int pop() {
int res = heap[1];
heap[1] = heap[size--];
sink(1);
return res;
}
private void swim(int x) {
while (x > 1 && heap[parent(x)] > heap[x]) {
swap(parent(x), x);
x = parent(x);
}
}
private void sink(int x) {
while (left(x) <= size || right(x) <= size) {
int min = x;
if (left(x) <= size && heap[left(x)] < heap[min]) {
min = left(x);
}
if (right(x) <= size && heap[right(x)] < heap[min]) {
min = right(x);
}
if (min == x) {
break;
}
swap(x, min);
x = min;
}
}
}
|
完善版优先级队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
| import java.util.Comparator;
import java.util.NoSuchElementException;
public class MyPriorityQueue<T> {
private T[] heap;
private int size;
private final Comparator<? super T> comparator;
@SuppressWarnings("unchecked")
public MyPriorityQueue(int capacity, Comparator<? super T> comparator) {
heap = (T[]) new Object[capacity + 1];
size = 0;
this.comparator = comparator;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
private int parent(int node) {
return node / 2;
}
private int left(int node) {
return node * 2;
}
private int right(int node) {
return node * 2 + 1;
}
private void swap(int i, int j) {
T temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
public T peek() {
if (isEmpty()) {
throw new NoSuchElementException("Priority queue underflow");
}
return heap[1];
}
public void push(T x) {
if (size == heap.length - 1) {
resize(2 * heap.length);
}
heap[++size] = x;
swim(size);
}
public T pop() {
if (isEmpty()) {
throw new NoSuchElementException("Priority queue underflow");
}
T res = heap[1];
swap(1, size--);
sink(1);
heap[size + 1] = null;
if ((size > 0) && (size == (heap.length - 1) / 4)) {
resize(heap.length / 2);
}
return res;
}
private void swim(int k) {
while (k > 1 && comparator.compare(heap[parent(k)], heap[k]) > 0) {
swap(parent(k), k);
k = parent(k);
}
}
private void sink(int k) {
while (left(k) <= size) {
int j = left(k);
if (j < size && comparator.compare(heap[j], heap[j + 1]) > 0) j++;
if (comparator.compare(heap[k], heap[j]) <= 0) break;
swap(k, j);
k = j;
}
}
@SuppressWarnings("unchecked")
private void resize(int capacity) {
assert capacity > size;
T[] temp = (T[]) new Object[capacity];
for (int i = 1; i <= size; i++) {
temp[i] = heap[i];
}
heap = temp;
}
public static void main(String[] args) {
MyPriorityQueue<Integer> pq = new MyPriorityQueue<>(3, Comparator.naturalOrder());
pq.push(3);
pq.push(1);
pq.push(4);
pq.push(1);
pq.push(5);
pq.push(9);
while (!pq.isEmpty()) {
System.out.println(pq.pop());
}
}
}
|