算法基础-数据结构基础(一)
2024-07-30 16:12:04 # 算法 # 数据结构基础 #算法

算法基础-数据结构基础(一)

数组

静态数组

静态数组就是连续的内存空间，int arr[10],我们知道了这块内存空间的首地址arr[10]，我们还知道每个元素的类型是int，也就是每个元素占内存空间大小是4个字节，那么这个int arr[10]就是10*4=40字节。

这种只要给一个数组的索引，我们就可以通过地址和索引算出元素的内存地址(在第几个字节)，直接获取元素值，所以通过索引直接查和改的时间复杂度就是O(1)。

在静态数组写入的时候，假如前四个索引都有元素了，我们想在第二个位置加一个元素，就需要后面的元素都往后挪一位，或者数组空间满了，arr[10]满了之后需要再写入一个元素，就需要扩容。这两种情况时间复杂度因为需要搬其他元素，都是O(n)。

如果数组在末尾插入元素并且索引没有满，时间复杂度是O(1)。

删除和插入的逻辑相同

总结

  • 增：
    • 在末尾追加元素：O(1)。
    • 在中间（非末尾）插入元素：O(N)。
  • 删：
    • 删除末尾元素：O(1)。
    • 删除中间（非末尾）元素：O(N)。
  • 查：给定指定索引，查询索引对应的元素的值，时间复杂度 O(1)。
  • 改：给定指定索引，修改索引对应的元素的值，时间复杂度 O(1)。

动态数组

动态数组底层还是静态数组，只是自动进行扩容而已，没区别，只是封装一层

ArrayList<Integer> arr = new ArrayList<>();

内存泄漏

删除元素的时候需要考虑内存泄漏的问题

java的垃圾回收是当这个对象再也无法访问到才会释放内存

1
2
3
4
5
6
7
8
9
10
// 删
public E removeLast() {
    E deletedVal = data[size - 1];
    // 删除最后一个元素
    // 必须给最后一个元素置为 null，否则会内存泄漏
    data[size - 1] = null;
    size--;

    return deletedVal;
}

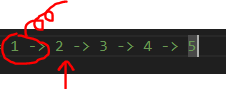
单双链表

单链表

数组是一块连续的内存空间。但是链表不是，链表可以分散在内存空间中的到处，通过指针将零散的内存块串联成一个链式结构

好处就是提高内存的利用效率，并且不许与考虑扩容和缩容的问题，不使用的时候就拆掉，使用时候就接上就好了

但是数组可以根据索引快速访问元素，但是链表不行

单链表的查询和修改只能遍历链表，找到索引对应的节点，然后进行修改

在单链表头添加元素可以直接获取单链表的头部指针，然后在头部插入新元素

在单链表的尾部添加元素，需要for遍历到单链表的尾部然后添加元素

在单链表中间添加元素，需要找到需要插入位置的前一个节点，然后插入新节点后挪动指针

在单链表删除元素就是把需要删除位置的前面一个节点的指针指向被删除的节点的下一个节点，也就是指针不指向删除的这个元素了，指向这个被删除元素的后面的一个元素

双链表

双链表在查询和更改的时候我们可以根据索引判断是靠近头还是靠近尾，来选择合适的方向进行遍历

在双链表头添加元素，需要把头指针指向新的节点，需要把新的节点的尾指针，指向之前的旧的头节点

1
2
3
4
5
6
7
8
9
// 创建一条双链表
DoublyListNode head = createDoublyLinkedList(new int[]{1, 2, 3, 4, 5});

// 在双链表头部插入新节点 0
DoublyListNode newHead = new DoublyListNode(0);
newHead.next = head;
head.prev = newHead;
head = newHead;
// 现在链表变成了 0 -> 1 -> 2 -> 3 -> 4 -> 5

在双链表的尾部插入元素，因为我们有尾节点的引用，就可以直接到尾节点，然后把尾指针指向新的这个尾节点，旧的尾节点的next指针指向新的尾节点

虚拟头尾节点：

创建双链表的时候就创建一个虚拟的头节点和虚拟的尾节点，无论双链表是否是空，这两个节点都存在，不会产生空指针的问题

创建一个虚拟的头尾节点的空的双链表：

dummyHead <-> dummyTail

插入元素后

dummyHead <-> 1 <-> 2 <-> 3 <-> dummyTail

内存泄漏

1
2
3
4
5
6
7
// 假设单链表头结点 head = 1 -> 2 -> 3 -> 4 -> 5

// 删除单链表头结点
head = head.next;

// 此时 head = 2 -> 3 -> 4 -> 5

这样的写法只是把头指针指向到了2元素上面，但是1的next指针还是连着2这个元素，所以最好还是要把删除节点的指针都置为null，1节点才会被垃圾回收
alt text

力扣题目

707题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
public class MyLinkedList {

    private Node head,tail;

    private int size;

    public class Node{
        int val;
        Node next;
        Node prev;

        Node(int val){
            this.val = val;
        }
    }

    public MyLinkedList() {
        head = new Node(0);
        tail = new Node(0);
        tail.prev = head;
        head.next = tail;

        size = 0;
    }

    public int get(int index) {
        if (index < 0 || index >= size) {
            return -1 ;
        }
        Node node = getNode(index);
        return node.val;

    }

    public void addAtHead(int val) {
        Node header = head.next;
        Node x = new Node(val);
        header.prev = x;
        head.next = x;
        x.prev = head;
        x.next = header;
        size++;

    }

    public void addAtTail(int val) {
        Node prev = tail.prev;
        Node x = new Node(val);
        prev.next = x;
        tail.prev = x;
        x.prev = prev;
        x.next = tail;
        size++;

    }

    public void addAtIndex(int index, int val) {
        if (index < 0 || index >= size) {
            return ;
        }
        Node inNode = getNode(index);
        Node inNodeprev = getNode(index - 1);
        Node x = new Node(val);
        inNode.prev = x;
        inNodeprev.next = x;
        x.prev = inNodeprev;
        x.next = inNode;
        size++;


    }

    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return ;
        }
        Node x = getNode(index);
        Node xjian = x.prev;
        Node xjia = x.next;
        xjian.next = xjia;
        xjia.prev = xjian;
        size--;
        x = null;


    }

    private Node getNode(int index) {
        Node node = head.next;
        for (int i = 0; i < index; i++) {
            node = node.next;
        }
        return node;
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */

队列-栈

前面说了计算机的两种存储方式，顺序存储和链式存储

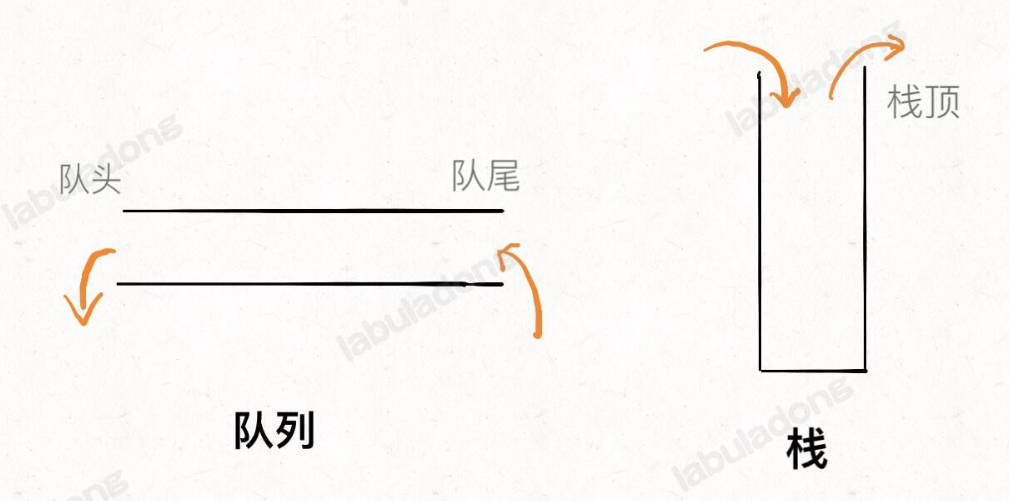
队列只能在一端插入元素，另一端删除元素；栈只能在某一端插入和删除元素

alt text

底层都是数组和链表实现的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 队列的基本 API
class MyQueue<E> {
    // 向队尾插入元素，时间复杂度 O(1)
    void push(E e);

    // 从队头删除元素，时间复杂度 O(1)
    E pop();

    // 查看队头元素，时间复杂度 O(1)
    E peek();

    // 返回队列中的元素个数，时间复杂度 O(1)
    int size();
}

// 栈的基本 API
class MyStack<E> {
    // 向栈顶插入元素，时间复杂度 O(1)
    void push(E e);

    // 从栈顶删除元素，时间复杂度 O(1)
    E pop();

    // 查看栈顶元素，时间复杂度 O(1)
    E peek();

    // 返回栈中的元素个数，时间复杂度 O(1)
    int size();
}

用链表实现队列-栈

双链表的尾部作为栈顶

时间复杂度都是 O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 用链表作为底层数据结构实现栈
public class MyLinkedStack<E> {
    private LinkedList<E> list = new LinkedList<>();

    // 向栈顶加入元素，时间复杂度 O(1)
    public void push(E e) {
        list.addLast(e);
    }

    // 从栈顶弹出元素，时间复杂度 O(1)
    public E pop() {
        return list.removeLast();
    }

    // 查看栈顶元素，时间复杂度 O(1)
    public E peek() {
        return list.getLast();
    }

    // 返回栈中的元素个数，时间复杂度 O(1)
    public int size() {
        return list.size();
    }
}

用链表实现队列

双链表的尾部作为队尾，把双链表的头部作为队头

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 用链表作为底层数据结构实现队列
public class MyLinkedQueue<E> {
    private LinkedList<E> list = new LinkedList<>();

    // 向队尾插入元素，时间复杂度 O(1)
    public void push(E e) {
        list.addLast(e);
    }

    // 从队头删除元素，时间复杂度 O(1)
    public E pop() {
        return list.removeFirst();
    }

    // 查看队头元素，时间复杂度 O(1)
    public E peek() {
        return list.getFirst();
    }

    // 返回队列中的元素个数，时间复杂度 O(1)
    public int size() {
        return list.size();
    }
}

环形数组技巧

环形数组技巧可以让我们用 O(1) 的时间在数组头部增删元素

数组是一块连续的内存空间，我们可以在逻辑上把这个数组变成环形的

1
2
3
4
5
6
7
8
// 长度为 5 的数组
int[] arr = new int[]{1, 2, 3, 4, 5};
int i = 0;
// 模拟环形数组，这个循环永远不会结束
while (i < arr.length) {
    System.out.println(arr[i]);
    i = (i + 1) % arr.length;
}

示例

假如说我们有一个长度是6，但是只有3个元素的数组
[1, 2, 3, _, _, _]

如果我们要在头部删除元素1，那么我们可以
[_, 2, 3, _, _, _]

如果我们要在头部添加元素4和5，就可以在头部添加4，尾部添加5
[4, 2, 3, _, _, 5]

用数组实现队列-栈

用数组实现栈的方式是把动态数组的尾部作为栈顶，然后调用动态数组的API

用数组实现栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 用数组作为底层数据结构实现栈
public class MyArrayStack<E> {
    private ArrayList<E> list = new ArrayList<>();

    // 向栈顶加入元素，时间复杂度 O(1)
    public void push(E e) {
        list.add(e);
    }

    // 从栈顶弹出元素，时间复杂度 O(1)
    public E pop() {
        return list.remove(list.size() - 1);
    }

    // 查看栈顶元素，时间复杂度 O(1)
    public E peek() {
        return list.get(list.size() - 1);
    }

    // 返回栈中的元素个数，时间复杂度 O(1)
    public int size() {
        return list.size();
    }
}

用数组实现队列

有了前文环形数组的内容，直接使用环形数组的内容就好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class MyArrayQueue<E> {
    private CycleArray<E> arr;

    public MyArrayQueue() {
        arr = new CycleArray<>();
    }

    public void push(E t) {
        arr.addLast(t);
    }

    public E pop() {
        return arr.removeFirst();
    }

    public E peek() {
        return arr.getFirst();
    }

    public int size() {
        return arr.size();
    }
}

双端队列原理

标准队列 只能在队尾插入元素，队头删除元素，而双端队列的队头和队尾都可以插入或删除元素

算法中双端队列用的不是很多

用链表实现双端队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MyListDeque<E> {
    private LinkedList<E> list = new LinkedList<>();

    // 从队头插入元素，时间复杂度 O(1)
    void addFirst(E e) {
        list.addFirst(e);
    }

    // 从队尾插入元素，时间复杂度 O(1)
    void addLast(E e) {
        list.addLast(e);
    }

    // 从队头删除元素，时间复杂度 O(1)
    E removeFirst() {
        return list.removeFirst();
    }

    // 从队尾删除元素，时间复杂度 O(1)
    E removeLast() {
        return list.removeLast();
    }

    // 查看队头元素，时间复杂度 O(1)
    E peekFirst() {
        return list.getFirst();
    }

    // 查看队尾元素，时间复杂度 O(1)
    E peekLast() {
        return list.getLast();
    }
}

用数组实现双端队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MyArrayDeque<E> {
    private CycleArray<E> arr = new CycleArray<>();

    // 从队头插入元素，时间复杂度 O(1)
    void addFirst(E e) {
        arr.addFirst(e);
    }

    // 从队尾插入元素，时间复杂度 O(1)
    void addLast(E e) {
        arr.addLast(e);
    }

    // 从队头删除元素，时间复杂度 O(1)
    E removeFirst() {
        return arr.removeFirst();
    }

    // 从队尾删除元素，时间复杂度 O(1)
    E removeLast() {
        return arr.removeLast();
    }

    // 查看队头元素，时间复杂度 O(1)
    E peekFirst() {
        return arr.getFirst();
    }

    // 查看队尾元素，时间复杂度 O(1)
    E peekLast() {
        return arr.getLast();
    }
}

哈希表

首先：

哈希表和我们常说的 Map（键值映射）不是同一个东西

Map是一个java接口，没有给出方法的具体实现，实现这个接口的类有很多：HashMap，TreeMap，LinkedHashMap等等。HashMap是Map的一个实现类

也就是说可以说HashMap的方法的复杂度都是o(1),但是不能说Map接口的复杂度都是o(1)

哈希表的基本原理

哈希表可以理解为一个加强版的数组。

数组可以通过索引（非负整数）在 O(1) 的时间复杂度内查找到对应元素。

哈希表是类似的，可以通过 key 在 O(1) 的时间复杂度内查找到这个 key 对应的 value。key 的类型可以是数字、字符串等多种类型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MyHashMap {

    private Object[] table;

    // 增/改，复杂度 O(1)
    public void put(K key, V value) {
        int index = hash(key);
        table[index] = value;
    }

    // 查，复杂度 O(1)
    public V get(K key) {
        int index = hash(key);
        return table[index];
    }

    // 删，复杂度 O(1)
    public void remove(K key) {
        int index = hash(key);
        table[index] = null;
    }

    // 哈希函数，把 key 转化成 table 中的合法索引
    // 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    private int hash(K key) {
        // ...
    }
}

几个关键点

  1. 哈希表的key是唯一的，value可以重复
    数组里面每个索引都是唯一的，不可能说你这个数组有两个索引 0。至于数组里面存什么元素，无所谓

  2. 哈希函数hash():

hash函数把任意长度的key转化成固定长度的输出，保证相同的key输出也要相同

  1. 哈希冲突：

哈希冲突也就是两个不同的key经过哈希函数得到了相同的索引，这种就是哈希冲突。

  1. 出现哈希冲突的解决办法：

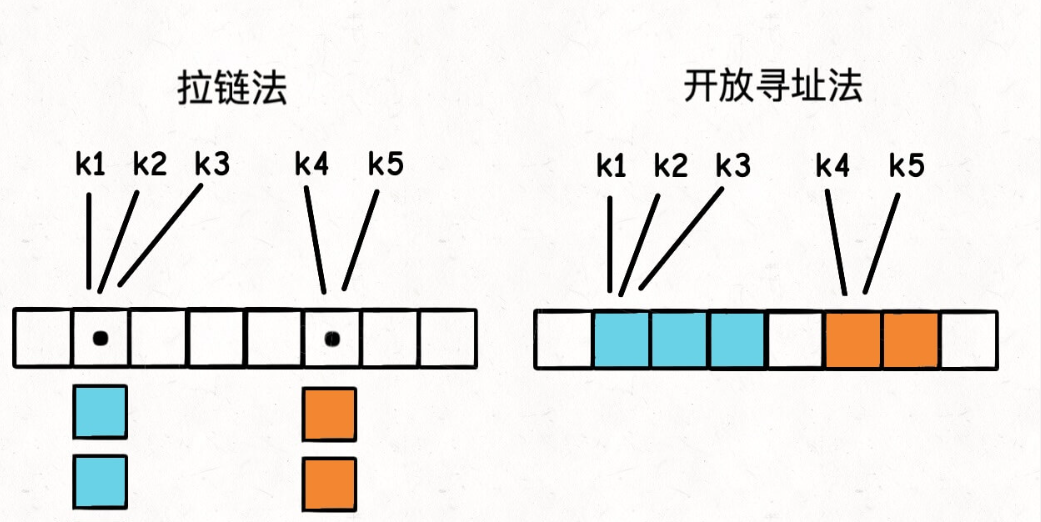
    出现哈希冲突有两种方法：

    alt text

    • 拉链法：底层数组不直接存储value，而是存储一个链表，当不同的key映射到一个索引，就把kv对存储在链表中
    • 线性探查法：key发现算出来的索引值已经被占了，就去index+1位置，如果还是被占了，就往后继续找，直到找到一个空位置为止

扩容和负载因子

负载因子：是一个哈希表装满的程度的度量，一般来说，负载因子越大，说明哈希表里面的 key-value 对越多，哈希冲突的概率就越大。

当哈希表中的元素达到负载因子，哈希表就会扩容，把哈希表底层的数组容量扩大，把数据搬到一个大的数组中

哈希表的key 必须是不可变的

总结

  1. 为什么哈希表的增删改查都是o(1)

    因为哈希表的底层是数组，时间复杂度来自于哈希函数计算和哈希冲突，保证哈希函数的复杂度是o(1)，解决哈希冲突问题，增删改查的复杂度就是o(1)

  2. 哈希表的遍历顺序为什么会变

    因为哈希表达到了负载因子就会扩容，扩容后，哈希函数计算的索引也会变

  3. 哈希表的增删改查的效率一定是o(1)吗

    哈希冲突是好解决的，哈希函数的计算复杂度如果使用了错误的key类型，使用了类似于arrayList这种作为key，那么哈希表的时间复杂度就会退化成o(n)

拉链实现哈希表解决哈希冲突

下面的哈希表的实现做一些简化：

  1. 我们实现的哈希表只支持 key 类型为 int，value 类型为 int 的情况，如果 key 不存在，就返回 -1。

  2. 我们实现的 hash 函数就是简单地取模，即 hash(key) = key % table.length。这样也方便模拟出哈希冲突的情况，比如当 table.length = 10 时，hash(1) 和 hash(11) 的值都是 1。

  3. 底层的 table 数组的大小在创建哈希表时就固定，不考虑负载因子和动态扩缩容的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import java.util.LinkedList;

// 用拉链法解决哈希冲突的简化实现
public class ExampleChainingHashMap {

    // 链表节点，存储 key-value 对儿
    // 注意这里必须存储同时存储 key 和 value
    // 因为要通过 key 找到对应的 value
    static class KVNode {
        int key;
        int value;

        // 为了简化，我这里直接用标准库的 LinkedList 链表
        // 所以这里就不添加 next 指针了
        // 你当然可以给 KVNode 添加 next 指针，自己实现链表操作
        public KVNode(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }


    // 底层 table 数组中的每个元素是一个链表
    private LinkedList<KVNode>[] table;

    public ExampleChainingHashMap(int capacity) {
        table = new LinkedList[capacity];
    }

    private int hash(int key) {
        return key % table.length;
    }

    // 查
    public int get(int key) {
        int index = hash(key);

        if (table[index] == null) {
            // 链表为空，说明 key 不存在
            return -1;
        }

        LinkedList<KVNode> list = table[index];
        // 遍历链表，尝试查找目标 key，返回对应的 value
        for (KVNode node : list) {
            if (node.key == key) {
                return node.value;
            }
        }

        // 链表中没有目标 key
        return -1;
    }

    // 增/改
    public void put(int key, int value) {
        int index = hash(key);

        if (table[index] == null) {
            // 链表为空，新建一个链表，插入 key-value
            table[index] = new LinkedList<>();
            table[index].add(new KVNode(key, value));
            return;
        }

        // 链表不为空，要遍历一遍看看 key 是否已经存在
        // 如果存在，更新 value
        // 如果不存在，插入新节点
        LinkedList<KVNode> list = table[index];
        for (KVNode node : list) {
            if (node.key == key) {
                // key 已经存在，更新 value
                node.value = value;
                return;
            }
        }

        // 链表中没有目标 key，添加新节点
        // 这里使用 addFirst 添加到链表头部或者 addLast 添加到链表尾部都可以
        // 因为 Java LinkedList 的底层实现是双链表，头尾操作都是 O(1) 的
        // https://labuladong.online/algo/data-structure-basic/linkedlist-implement/
        list.addLast(new KVNode(key, value));
    }

    // 删
    public void remove(int key) {
        LinkedList<KVNode> list = table[hash(key)];
        if (list == null) {
            return;
        }

        // 如果 key 存在，则删除
        // 这个 removeIf 方法是 Java LinkedList 的方法，可以删除满足条件的元素，时间复杂度 O(N)
        list.removeIf(node -> node.key == key);
    }
}

线性探查法

线性探查法暂时省略，后续算法使用到再进行补充

哈希集合

哈希表的键，其实就是哈希集合

哈希集合主要就是做去重，因为哈希表的键是不重复的。可以在 O(1) 的时间增删元素，可以在 O(1) 的时间判断一个元素是否存在

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import java.util.HashMap;

public class MyHashSet<K> {
    // 随便创建一个值，作为 value 占位符
    private static final Object PRESENT = new Object();
    // 底层 HashMap，我这里直接用标准库了，你用前文自己实现的哈希表也可以
    private final HashMap<K, Object> map = new HashMap<>();

    public void add(K key) {
        // 向哈希表添加一个键值对
        map.put(key, PRESENT);
    }

    public void remove(K key) {
        // 从哈希表中移除键 key
        map.remove(key);
    }

    public boolean contains(K key) {
        // 判断哈希表中是否包含键 key
        return map.containsKey(key);
    }

    public int size() {
        return map.size();
    }
}
上一页
2024-07-30 16:12:04 # 算法 # 数据结构基础 #算法
下一页